Image 1: 3 steps on the construction of the fractal Tetra-circle.
This section does not intends to explore formaly the concept of fractal, but to present a didactic approach that can be used with middle, high school and undergraduate students to introduce concepts like: algorithms; geometric progressions (gp); and series.
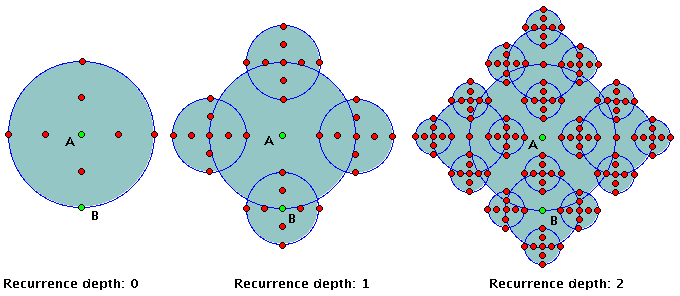
A fractal must present a characteristic of "self-semblance", which means that if it was possible to put a magnifying glass in a given piece of it, the resulting image would be identical to the original. Below we present finite representations of 2 fractals that are discussed in detail on the links.

This type of didactic approach can be improved by the use of a Interactive Geometry System that allows the construction of scripts (or geometric algorithms), and even more if the system have recurrence, like iGeom. The principle of this approach is the identification of the basis to the construction of geometric fractals and in which these objects must be applyed the recurrence.
The big advantage of the recurrence here is to allow the student to focus just on the fundaments of the construction, in which she does not need to apply the script (without recurrence) too many times (which would be necessary to get good representations of the fractal). Just for being new, mainly to high school students, probably the reader already knows one recorrent function: the factorial function,
| Factorial | fact: IN -> IN |
| fact(n) := { 1, se n=0; n * fact(n-1), se n>0 }. | |
| (note that the own function - underlined - is called in its definition - this is the recurrence) |
With the use of scripts recurrents, one can obtain geometric constructions that describe fractals, and from the properties of these constructions can explore the concepts listed above. For example, the concept of algorithm (or even of software programming) can be introduced challenging the students to deduce the scripts that could generate a given fractal. Recovering the idea of Seymour Papert with the introduction of the Logo language.
The work with students of middle school can follow the black-box method, providing a ready-to-use script and asking them to discover the specific properties based on counting (for example, on the fractal tetra-circle, if applyed typing k, a positive integer, how many circumferences will show up?).
On the following is presented two examples of geometric fractals. On the first one the steps for the construction are more detailed.