.: Sierpinski's Triangle Fractal :.
The Sierpinski's Triangle is a fractal usually defined from a triangle.
The construction here presented will use two points as parameters.
As the details for the definition of a recurring script were explored on the fractal
Tetra-circle, on this it will be given only the steps
for the construction of the recurrent script which gives the desired fractal.
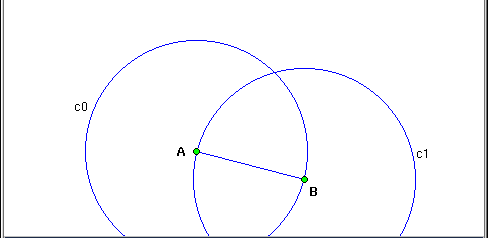
- Given two points (just open the script recorder after these two points being on the drawing area),
build the circumferences c0 of center A, passing through B and
c1 of center B, passing through A. Build also the segment AB.
- Build the point C, intersection "north" between c0 and c1.
Build the segments AC and BC.
- Build the midpoints D, E, F, respectively of AB, BC and AC.
In this moment the "fractal's base" is ready, one should now note the recurrence on the pairs of points
AD, DB and FE (respecting the script's order of construction, the triangle's base,
that can be found in the top of the script's recording window - if the order of the first recurrence is changed
to DA it will implies that the fractal's growing will be on the "left corner" and it will be misshaped,
going "downwards").
For the script to give "cleaner" representations of the fractal it is convenient to hide the cincunferences
c0 and c1 and the labels D, E and F (for that the objects must be selected and then
click on the button to hide  ).
).
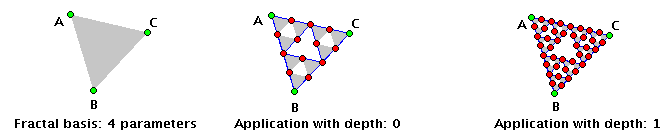
One can deduce a Sierpinski's fractal a little richier, using as parameters 3 points and the polygon
formed by those points. This model represents bettre the idea of the Sierpinski's fractal, which is at each level
eliminates the "central third" of the triangle.
On the image below are represented three moments of the contruction of this richier fractal, that uses
4 parameter (Point, Point, Point, Polygon). On the left there are the 4 initial objects (which will be parameters),
on the middle it is the fractal's base, on the moment that will be applyed the 3 recurrences. On the right it is
on application of the script using the recurrence depht of 1.

 ).
).



 ).
).