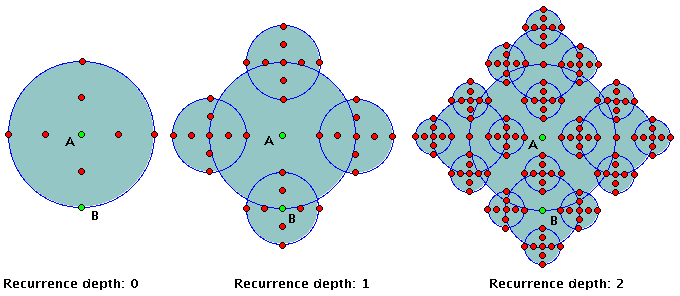
 | Figure 1: 3 representations of the proposed fractal, with recurrence depths of 0, 1 and 2 respectively. |
 | Figure 1: 3 representations of the proposed fractal, with recurrence depths of 0, 1 and 2 respectively. |
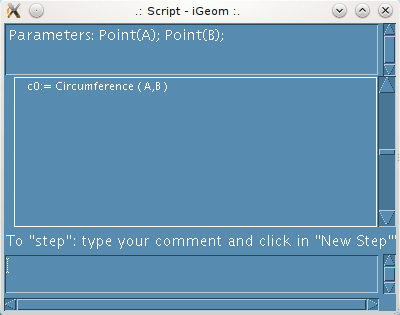 |
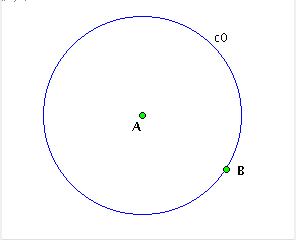 | Figure 2: first operation followed (the 2 points not built by the script => parameters) |
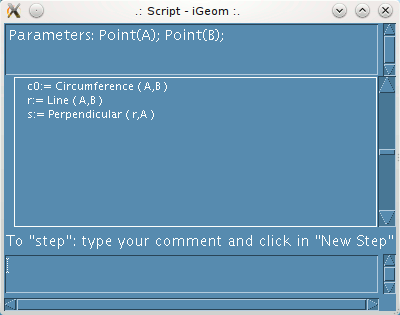 |
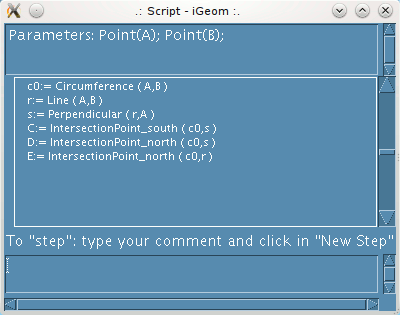
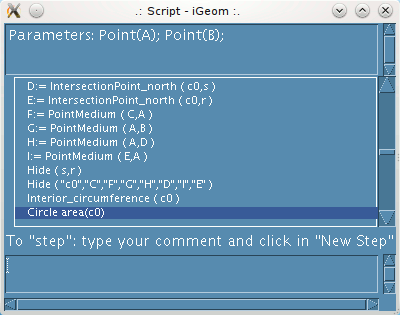
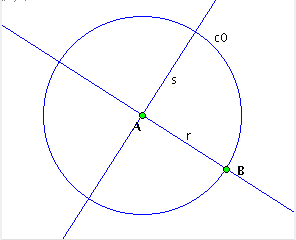 | Figure 3: on the left the script window with the second and third operations followed on the right the corresponding construction |
 |
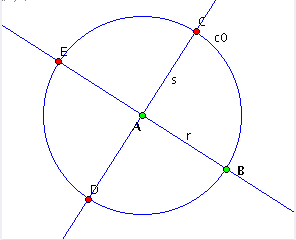 | Figure 4: three new steps followed (construction of the intersections) |
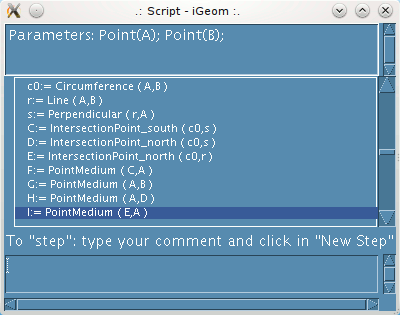 |
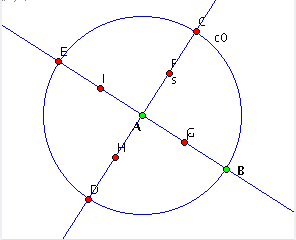 | Figure 5: four new steps (construction of the midpoints) |
 |
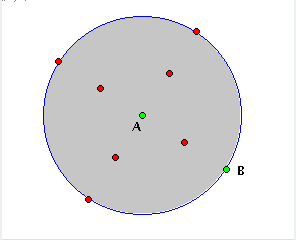 | Figure 6: four new steps (editing steps) |
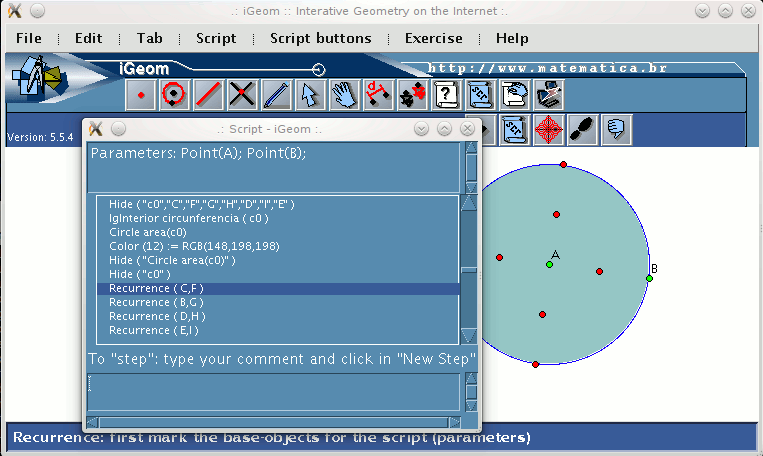 | Figure 7: the last 4 instructions is the anotation of the recursive calls |
 | Figure 8: window to choose the recurrence depth |
| depth | number of objects | total |
| 0: | 2+12 * (40) | = 2+12 |
| 1: | 2+12 * (40+41) | = 2+60 |
| 2: | 2+12 * (40+41+42) | = 2+252 |
| 3: | 2+12 * (40+41+42+43) | = 2+1020 |
| Applet 1: on the first script button is the Tetra-circle fractal's algorithm. |
| Applet 2: representations for the Tetra-circle fractal. |