Dos três problemas famosos da Antigüidade, o da trissecção do ângulo é talvez o que tenha maior número de provas falsas. Existem muitas "provas" de como trissectar um ângulo arbitrário usando régua e compasso; porém são todas incorretas já que esta construção é impossível. Saber que a prova é incorreta e encontrar o erro são dois problemas diferentes pois o erro pode ser sutil e difícil de ser encontrado.

O problema da trissecção difere dos outros dois problemas clássicos. Primeiramente porque não há nenhuma referência sobre quando este problema começou a ser estudado. Segundo, porque este é um problema bastante diferente, já que é impossível quadrar qualquer círculo e dobrar qualquer cubo enquanto que alguns ângulos são possíveis de serem trissectados usando instrumentos euclideanos (por exemplo, para trissectar um ângulo reto basta construir um triângulo equilátero). Mas não há nenhuma solução para ângulos quaisquer.

A seguir será descrito o problema das inclinações, ao qual o problema da trissecção de um ângulo qualquer foi reduzido.

Dado um ângulo qualquer deve-se desenhar um retângulo ACBD de modo que AB seja uma de suas diagonais.

Agora considere uma reta por B e cortando CA em E e o prolongamento de DA em F de tal modo que EF=2(BA).

Seja G o ponto médio de EF, podemos provar que GA=GQ=AB e que o ângulo ABG=AGB.

Como AGB é ângulo externo do triângulo AGQ temos ABG=2GFA=2GBC. Assim ABC=3GBC, pois ABC=ABG+GBC.

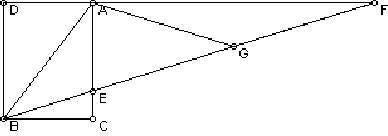
Este método de trissecção, na verdade, não é possível com régua e compasso euclideanos pois não conseguimos traçar a linha EF por B. Assim, o problema apenas foi traduzido num outro.

É possível solucionar este problema teoricamente usando cônicas, cubicas, métodos mecânicos ou curvas superiores.

A maioria dos historiadores de matemática acreditam que Arquimedes resolveu este problema usando a espiral de Arquimedes.

Nicomedes que viveu aproximadamente na mesma época que Arquimedes também produziu uma solução através de uma curva, a chamada conchóide.

Outra maneira pela qual a trissecção pode ser efetuada é através da trissectriz de Hípias.