A conchóide de Nicomedes é usada na
trissecção de um ângulo e na
duplicação do cubo. Ela pode ser construída usando um dispositivo mecânico que será descrito a seguir.
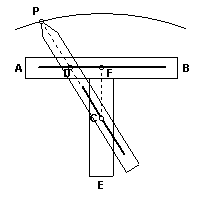
Seja AB uma régua com uma abertura paralela ao seu comprimento, FE uma segunda régua fixada perpendicularmente a AB, com um pólo C fixado nela. A terceira régua PC, que aponta para P, também tem uma abertura paralela ao seu comprimento com ajuste no ponto C. D é o pólo fixado em PC que pode mover-se na abertura de AB.
Se a régua PC se move de forma que o ponto D descreve o comprimento da abertura em AB, a extremidade P da régua descreve a curva que é chamada conchóide.
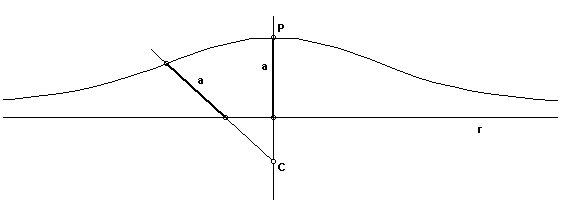
A propriedade fundamental da conchóide é que se desenharmos qualquer raio vetor de C para a curva, como CP, o comprimento entre a intersecção com a curva e a intersecção com a reta r é constante.
Como foi feito na
trissecção do ângulo, para dividir um ângulo qualquer em três partes iguais faremos o seguinte:
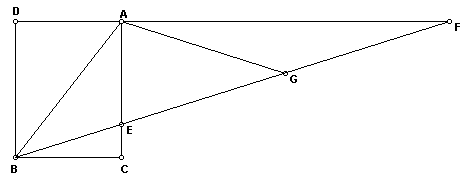
Seja ABC um ângulo qualquer que desejamos trissectar. Deve-se desenhar um retângulo ACBD de modo que AB seja uma de suas diagonais.
Agora considere uma reta por B e cortando CA em E e o prolongamento de DA em F de tal modo que EF = 2 (BA).
Seja G o ponto médio de EF, podemos provar que GA = GF = AB e que o ângulo ABG = AGB.
Como AGB é ângulo externo do triângulo AGF temos:
ABG = 2 GFA = 2 GBC
Assim ABC = 3 GBC, pois ABC = ABG + GBC.
Portanto para trissectar o ângulo ABC, basta traçar EF=2AB, porém apenas com régua e compasso euclidianos é impossível; sendo B, E e F pontos colineares. Assim este problema foi solucionado utilizando a conchóide.
Seja ABC o ângulo que queremos trissectar, com AB = a e seja a conchóide abaixo desenhada de tal forma que AD'= 2 AB = 2 a (pela propriedade explicada acima).
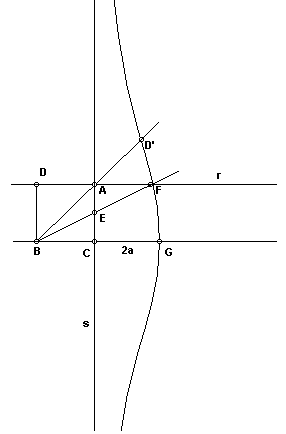
Traçando uma reta
r que passa por
A e é perpendicular a reta
s.
Chamamos de
F a intersecção de
r com a conchóide e traçamos o segmento
BF. Novamente
EF = AD = CG = 2a. Portanto encontramos o segmento
EF = 2a acima procurado e o ângulo
ABC esta trissectado.
Abaixo a mesma ilustração, desta vez utilizando o programa de
Geometria Interativa
iGeom.
Ilustração dinâmica da Conchóide de Nicomedes: clique sobre os pontos
C ou F, solte o botão do "mouse" e mova-o pela tela.







