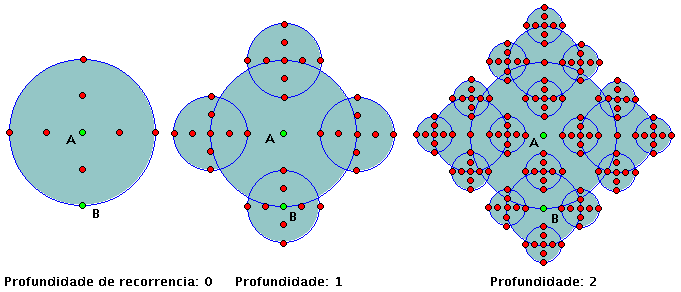
 | Figura 1: 3 representações do fractal proposto nesta página, com profundidades de recorrência respectivamente 0, 1 e 2. |
 | Figura 1: 3 representações do fractal proposto nesta página, com profundidades de recorrência respectivamente 0, 1 e 2. |
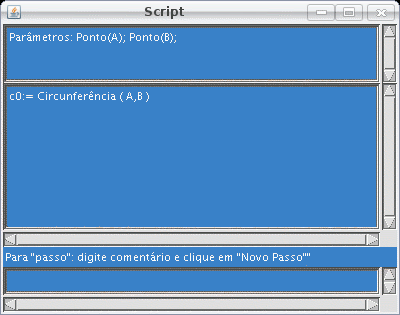 |
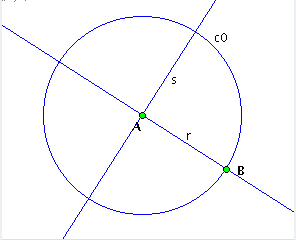
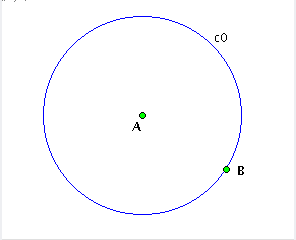 | Figura 2: primeira operação anotada (usou 2 pontos não construídos pelo script => serão parâmetros) |
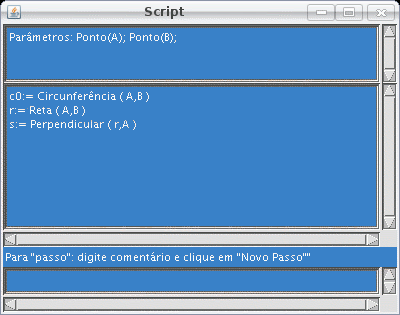 |
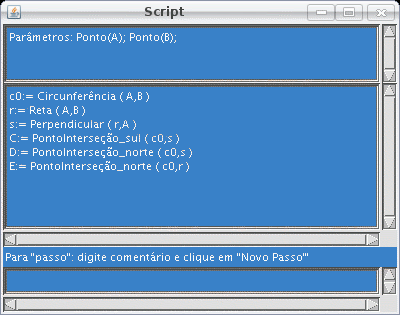
 | Figura 3: à esquerda a janela de script com segunda e terceira operações anotadas e à direita a construção correspondente |
 |
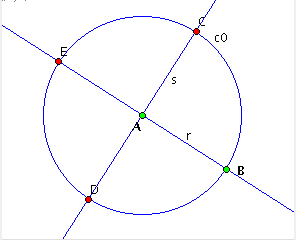 | Figura 4: três novos passos anotadas (relativos às construções de interseções) |
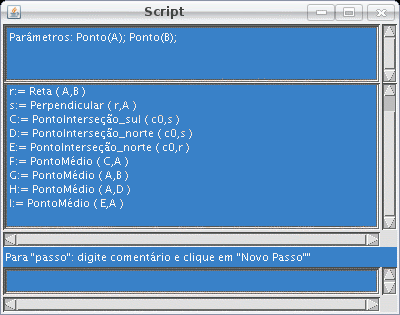 |
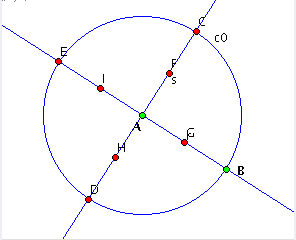 | Figura 5: quatro novos passos anotadas (relativos às construções de pontos médios) |
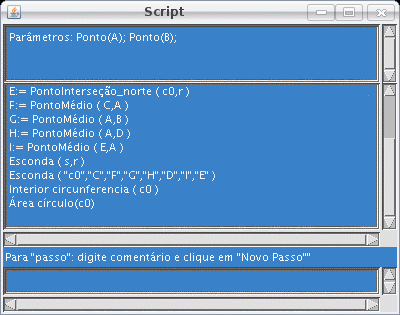 |
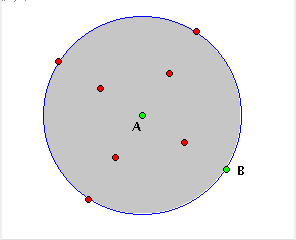 | Figura 6: quatro novos passos anotadas (relativos às construções de pontos médios) |
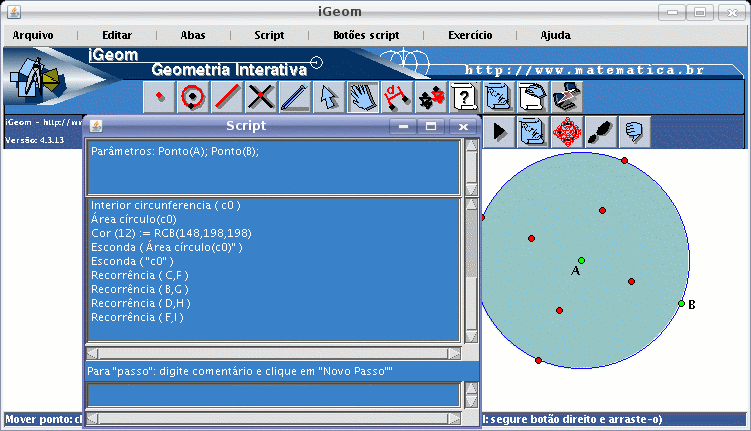 | Figura 7: anotação das últimas operações de edição e das 4 chamadas recorrentes |
 | Figura 8: janela para escolher a profundidade de recorrência. |
| profundidade | número de objetos | <total | /tr>
| 0: | 2+12 * (40) | = 2+12 |
| 1: | 2+12 * (40+41) | = 2+60 |
| 2: | 2+12 * (40+41+42) | = 2+252 |
| 3: | 2+12 * (40+41+42+43) | = 2+1020 |
| Applet 1: no primeiro botão de script já existe o algoritmo para gerar o fractal Tetra-círculo. |
| Applet 2: representações para o fractal Tetra-círculo, com aplicações do script. |