Hipias desenvolveu uma curva mecânica chamada trissectriz ou quadratriz. Esta curva recebeu este nome porque serve tanto para trissectar um ângulo como para quadrar um círculo.
A trissectriz é uma curva que não pode ser traçada apenas com régua e compasso euclidiano.
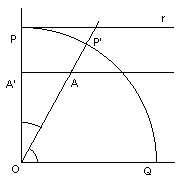
Essa curva é definida da seguinte maneira: dado um raio OP, suponha ele girando uniformemente até chegar na posição OQ, e ao mesmo tempo a reta r também se deslocando uniformemente até a posição OQ. Depois de um mesmo tempo, o raio estará na posição OP´ e o segmento na posição A´A, sendo A o ponto de intersecção desses segmentos, o lugar descrito por A durante esses movimentos será a trissectriz de Hipias.
Seja
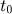
segundos o tempo que leva P para girar até Q. Então
arco percorrido em 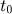 segundos =
segundos =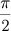 arco percorrido em 1 segundo =
arco percorrido em 1 segundo =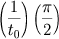 arco percorrido em t segundos é
arco percorrido em t segundos é 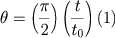
Da mesma forma, em
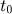
segundos, o ponto A´ percorre PO, em 1 segundo, percorre
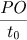
donde, em t segundos percorre
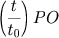
.
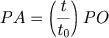
.
Temos que
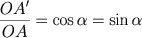
. Chamando OA = a temos
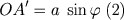
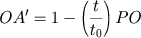
De (1) temos
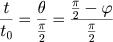
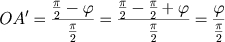
Voltando a (2) temos:
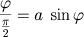
Se assumirmos que uma tal curva esta desenhada, podemos trissectar um ângulo qualquer
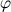
, da seguinte forma
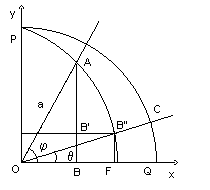
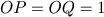
Dado
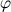
:
(1) Cortamos com a curva em A.
(2) Trazemos a perpendicular AB.
(3) Dividimos o segmento AB de modo que
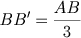
(usando Teorema de Tales).
(4) Trazemos a paralela por B' a OX e cortamos a trissectriz em B''.
(5) Trazemos OB'' que corta a circunferência em C.
De fato, temos que:
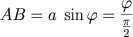 e
e 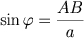
Da mesma forma:
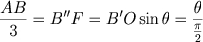
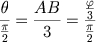
donde
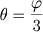
Note que se inicialmente dividirmos AB em n partes iguais iremos obter um ângulo
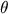
tal que
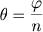
.
A aplicação desta curva ao problema da quadratura do círculo é mais complicada e não será feita aqui. O leitor interessado pode consultar o livro de T.L.Heath.A History of Greek Mathematics, Dover Publication, Inc, Nova Iorque, 1981, vol I, pp 227/228.





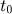 segundos o tempo que leva P para girar até Q. Então
segundos o tempo que leva P para girar até Q. Então
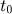 segundos =
segundos =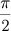
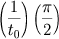
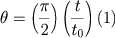
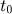 segundos, o ponto A´ percorre PO, em 1 segundo, percorre
segundos, o ponto A´ percorre PO, em 1 segundo, percorre 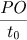 donde, em t segundos percorre
donde, em t segundos percorre 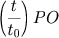 .
. 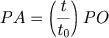 .
Temos que
.
Temos que 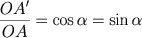 . Chamando OA = a temos
. Chamando OA = a temos
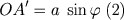
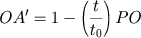
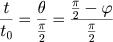
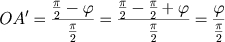 Voltando a (2) temos:
Voltando a (2) temos:
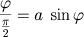
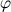 , da seguinte forma
, da seguinte forma

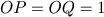
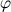 :
(1) Cortamos com a curva em A.
(2) Trazemos a perpendicular AB.
(3) Dividimos o segmento AB de modo que
:
(1) Cortamos com a curva em A.
(2) Trazemos a perpendicular AB.
(3) Dividimos o segmento AB de modo que 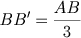 (usando Teorema de Tales).
(4) Trazemos a paralela por B' a OX e cortamos a trissectriz em B''.
(5) Trazemos OB'' que corta a circunferência em C.
De fato, temos que:
(usando Teorema de Tales).
(4) Trazemos a paralela por B' a OX e cortamos a trissectriz em B''.
(5) Trazemos OB'' que corta a circunferência em C.
De fato, temos que:
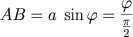 e
e 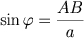
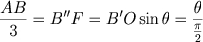
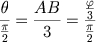
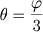 Note que se inicialmente dividirmos AB em n partes iguais iremos obter um ângulo
Note que se inicialmente dividirmos AB em n partes iguais iremos obter um ângulo 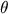 tal que
tal que 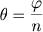 .
A aplicação desta curva ao problema da quadratura do círculo é mais complicada e não será feita aqui. O leitor interessado pode consultar o livro de T.L.Heath.A History of Greek Mathematics, Dover Publication, Inc, Nova Iorque, 1981, vol I, pp 227/228.
.
A aplicação desta curva ao problema da quadratura do círculo é mais complicada e não será feita aqui. O leitor interessado pode consultar o livro de T.L.Heath.A History of Greek Mathematics, Dover Publication, Inc, Nova Iorque, 1981, vol I, pp 227/228.