Giuseppe Peano, é um autor italiano, cujo nome é lembrado até hoje em conexão com os axiomas por ele introduzidos, dos quais dependem tantas construções rigorosas da álgebra e da análise. O que motivou seu trabalho foi o desejo de expressar toda a matemática em termos de um cálculo lógico. Em seu
Formulaire de Mathématiques, que contém cinco volumes ( escrito com a participação de colaboradores ) publicados a partir de 1894, desenvolveu uma linguagem formalizada que continha não só a lógica matemática como todos os ramos mais importantes da matemática. Atraiu um grande número de colaboradores e discípulos pelo fato de evitar o uso de uma linguagem metafísica e de introduzir símbolos: tais como

(pertence à classe de),

(soma lógica ou união),

(produto lógico ou intercessão) e

(contém) - muitos deles usados até hoje. Para seus fundamentos da aritmética ele escolheu três conceitos primitivos - zero, número ( que, no contexto, se refere a inteiros positivos), e a relação "é sucessor de" - satisfazendo aos cinco postulados seguintes:
- Zero é um número.
- Se a é um número, o sucessor de a é um número.
- Zero não é o sucessor de um número.
- Dois números cujos sucessores são iguais são eles próprios iguais.
- Se um conjunto S de números contém o zero e também o sucessor de todo número de S, então todo número está em S.
Em 1888, introduziu a definição axiomática de espaço vetorial, chamando de sistemas lineares.
Os axiomas de Peano, foram formulados pela primeira vez em 1889 na
Arithmetices Principia nova methodo exposita, que representava a tentativa de reduzir a aritmética comum a puro simbolismo formal. Peano exprimia os postulados em símbolos, em vez das palavras que usamos. O método postulacional atingiu novo nível de precisão, sem ambigüidade de sentido e sem hipóteses ocultas. Ele também desenvolveu a lógica simbólica.
Em 1890, Peano mostrou que a matemática podia surpreender o senso comum quando construiu curvas continuas que enchem o espaço - isto é, curvas dadas por equações paramétricas x = f(t), y = g(t), onde f e g são funções reais contínuas no intervalo
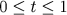
, cujos pontos preenchem completamente o quadrado unitário
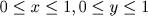
. Esse paradoxo combina perfeitamente com a descoberta de
Cantor de que não há mais pontos no quadrado unitário que no segmento de reta unitário. Porém, em 1903, Peano se distraiu com a invenção da linguagem internacional que ele chamou
Interlíngua ou
Latino sine flexione, com vocabulário tirado do latim, francês, inglês e alemão. Esse movimento foi mais efêmero que sua estrutura axiomática da aritmética.
No final do século XIX, com a aritmetização da análise e os axiomas de Peano, a maior parte da matemática conseguiu base estritamente axiomática. Peano foi um dos precursores do logicismo cuja expressão definitiva é a monumental obra
Principia Mathematica de Whitchead e Russell.




 (pertence à classe de),
(pertence à classe de),  (soma lógica ou união),
(soma lógica ou união),  (produto lógico ou intercessão) e
(produto lógico ou intercessão) e  (contém) - muitos deles usados até hoje. Para seus fundamentos da aritmética ele escolheu três conceitos primitivos - zero, número ( que, no contexto, se refere a inteiros positivos), e a relação "é sucessor de" - satisfazendo aos cinco postulados seguintes:
(contém) - muitos deles usados até hoje. Para seus fundamentos da aritmética ele escolheu três conceitos primitivos - zero, número ( que, no contexto, se refere a inteiros positivos), e a relação "é sucessor de" - satisfazendo aos cinco postulados seguintes:
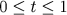 , cujos pontos preenchem completamente o quadrado unitário
, cujos pontos preenchem completamente o quadrado unitário 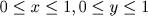 . Esse paradoxo combina perfeitamente com a descoberta de Cantor de que não há mais pontos no quadrado unitário que no segmento de reta unitário. Porém, em 1903, Peano se distraiu com a invenção da linguagem internacional que ele chamou Interlíngua ou Latino sine flexione, com vocabulário tirado do latim, francês, inglês e alemão. Esse movimento foi mais efêmero que sua estrutura axiomática da aritmética.
No final do século XIX, com a aritmetização da análise e os axiomas de Peano, a maior parte da matemática conseguiu base estritamente axiomática. Peano foi um dos precursores do logicismo cuja expressão definitiva é a monumental obra Principia Mathematica de Whitchead e Russell.
. Esse paradoxo combina perfeitamente com a descoberta de Cantor de que não há mais pontos no quadrado unitário que no segmento de reta unitário. Porém, em 1903, Peano se distraiu com a invenção da linguagem internacional que ele chamou Interlíngua ou Latino sine flexione, com vocabulário tirado do latim, francês, inglês e alemão. Esse movimento foi mais efêmero que sua estrutura axiomática da aritmética.
No final do século XIX, com a aritmetização da análise e os axiomas de Peano, a maior parte da matemática conseguiu base estritamente axiomática. Peano foi um dos precursores do logicismo cuja expressão definitiva é a monumental obra Principia Mathematica de Whitchead e Russell.