Os pitagóricos relacionavam a geometria e a aritmética através dos
números figurados, isto é, expressavam os números através de pontos em determinadas configurações geométricas.
Uma das configurações usadas era distribuir os pontos formando retângulos. Por exemplo, o número 12 seria representado assim:

Alguns números só podiam ser representados numa linha, e nunca num retângulo, por exemplo o número 5:

Estes números eram considerados
"primários" (de onde deriva a palavra
primos hoje utilizada), os outros números eram compostos.
Atualmente, usamos a seguinte definição formal: um número inteiro
p chama-se
primo se tem exatamente dois divisores positivos, 1 e
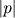
.
Desta forma o número 0 é excluído, pois tem infinitos divisores positivos, e os inteiros 1 e -1 que têm um único divisor positivo.
Um número diferente de 0, 1 e -1 que não é primo, chama-se
composto.
Note que, se um inteiro não nulo
a é composto, ele admite um divisor b tal que
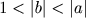
. Um divisor nessas condições diz-se um divisor próprio de
a.
O
Teorema fundamental da aritmética estabeleceu que todo número inteiro pode-se escrever como um produto único de
números primos. Desta forma, os
números primos teriam, na aritmética, um papel semelhante ao dos átomos na estrutura da matéria: por multiplicação deles pode-se construir todos os números inteiros, a partir deles.






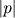 .
Desta forma o número 0 é excluído, pois tem infinitos divisores positivos, e os inteiros 1 e -1 que têm um único divisor positivo.
Um número diferente de 0, 1 e -1 que não é primo, chama-se composto.
Note que, se um inteiro não nulo a é composto, ele admite um divisor b tal que
.
Desta forma o número 0 é excluído, pois tem infinitos divisores positivos, e os inteiros 1 e -1 que têm um único divisor positivo.
Um número diferente de 0, 1 e -1 que não é primo, chama-se composto.
Note que, se um inteiro não nulo a é composto, ele admite um divisor b tal que 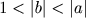 . Um divisor nessas condições diz-se um divisor próprio de a.
O Teorema fundamental da aritmética estabeleceu que todo número inteiro pode-se escrever como um produto único de números primos. Desta forma, os números primos teriam, na aritmética, um papel semelhante ao dos átomos na estrutura da matéria: por multiplicação deles pode-se construir todos os números inteiros, a partir deles.
. Um divisor nessas condições diz-se um divisor próprio de a.
O Teorema fundamental da aritmética estabeleceu que todo número inteiro pode-se escrever como um produto único de números primos. Desta forma, os números primos teriam, na aritmética, um papel semelhante ao dos átomos na estrutura da matéria: por multiplicação deles pode-se construir todos os números inteiros, a partir deles.