Durante séculos, os matemáticos procuraram fórmulas para resolver, usando radicais, operações algébricas de grau superior ao quarto. Embora pouco úteis do ponto de vista prático, devido às dificuldades técnicas para calcular efetivamente esses radicais, trariam -pelo menos- o conforto de saber que os números complexos seriam suficientes para todos os "cálculos algébricos". (Este conforto seria atingido por outras vias quando
Gauss publicou, em 1799, a demonstração do
Teorema Fundamental da Álgebra, na sua tese de doutorado).
Os primeiros passos na direção correta se devem ao matemático francês
Joseph Louis Lagrange que, estudando sistematicamente as fórmulas já conhecidas, foi levado a considerar permutações entre as raízes em torno de 1777. Lagrange não resolveu o problema, mas sua obra teve o mérito indiscutido de assinalar a direção correta, preparando o caminho para os seus sucessores. Um trabalho semelhante foi desenvolvido, na mesma época por Van der Monde.
Paolo Ruffini, que se considerava, em certa forma, discípulo de Lagrange, tentou provar que a equação geral de grau superior ao quarto não é resolúvel por radicais, mas seus esforços, embora corretos, não foram considerados conclusivos, usando também extensamente as permutações. A primeira demonstração rigorosa da impossibilidade de resolver a equação de quinto grau usando radicais é devida ao matemático Niels Henrik Abel, e até hoje este resultado é um dos mais célebres da matemática.
Os avanços conceituais mais importantes, porém, foram feitos por
Evariste Galois (1811-1832), tanto do ponto de vista da teoria das equações como da teoria de grupos.
No seu trabalho, ele procurava dar um critério para decidir quando uma dada equação é, ou não, solúvel por radicais. Porém ele percebeu claramente que tinha descoberto princípios gerais de uma importância muito maior. Isto fica claro na sua afirmação de que estava apresentando
"os princípios gerais e apenas uma aplicação".
Ele utilizava a palavra permutação no mesmo sentido em que Cauchy empregava substituição e foi o primeiro a usar a palavra
grupo no sentido técnico de conjunto fechado por multiplicação (note que, neste contexto, como se trata de conjuntos finitos e as permutações são inversíveis, isto é suficiente para caracterizar um grupo):
"se temos num mesmo grupo as permutações S e T, temos a certeza de que temos a permutação ST".
Mostrou que as propriedades algébricas mais importantes de uma dada equação eram refletidas por um grupo univocamente associado à equação, o chamado
grupo da equação. Para descrever algumas destas propriedades em termos dos grupos ele introduziu o conceito de subgrupo normal, que chamava de
distinguido ou
invariante. Em continuação ele introduz também o conceito de
grupo solúvel e prova que uma dada equação é resolúvel por radicais se o grupo dessa equação é solúvel.
Nos anos de 1844-1846
Augustin-Louis Cauchy publicou uma seqüência de artigos sobre permutações. Em particular, em 1844 dá uma definição do conceito de grupo (embora, como veremos, neste aspecto já tinha sido antecipado por
Galois):
Dada uma ou mais substituições que envolvem os mesmos elementos x, y, x,...chamo o produto destas substituições, por si mesmas ou por outras, em qualquer ordem , de
substituição derivada. As substituições dadas, junto com as derivadas, formam o que chamou de
sistema de substituições conjugadas.
Entre muitos resultados obtidos por
Cauchy, podemos citar os seguintes, que provavelmente são conhecidos o leitor:
· Toda permutação par é produto de ciclos de comprimento 3.
· Se um primo p é um divisor da ordem de um grupo, então o grupo contém um subgrupo de ordem p. (Este resultado é conhecido hoje como Teorema de Cauchy, embora tenha sido enunciado, pela primeira vez, sem demonstração, por Galois).
· O conjunto das substituições que comutam com uma dada substituição forma um subgrupo (o
centralizador do elemento).
· Determinou todos os subgrupos de
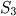
,
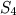
,
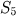
,
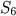
(cometendo um erro em
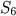
).
Para um estudo detalhado das contribuições de
Cauchy nesta área veja A. Dahan, Les Travaux de Cauchy sur lês Substitutions. Etude de son approche du concept de groupe,
Arch. Hist. Exact Sci., 23 (1980), 279-319; também pode ser interessante consultar J. Burns, The Foundation Period in the History of Group Theory,
Amer. Math.Mothly, 20 (1913), 141-148.




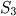 ,
, 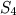 ,
, 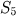 ,
, 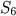 (cometendo um erro em
(cometendo um erro em 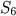 ).
Para um estudo detalhado das contribuições de Cauchy nesta área veja A. Dahan, Les Travaux de Cauchy sur lês Substitutions. Etude de son approche du concept de groupe, Arch. Hist. Exact Sci., 23 (1980), 279-319; também pode ser interessante consultar J. Burns, The Foundation Period in the History of Group Theory, Amer. Math.Mothly, 20 (1913), 141-148.
).
Para um estudo detalhado das contribuições de Cauchy nesta área veja A. Dahan, Les Travaux de Cauchy sur lês Substitutions. Etude de son approche du concept de groupe, Arch. Hist. Exact Sci., 23 (1980), 279-319; também pode ser interessante consultar J. Burns, The Foundation Period in the History of Group Theory, Amer. Math.Mothly, 20 (1913), 141-148.