A duplicação do cubo é um dos "três problemas famosos (ou clássicos)"da antigüidade. Não sabemos precisamente quando e por quem este problema foi formulado pela primeira vez, pois existem vários relatos a respeito. Uma das versões diz que como os délios haviam sido atingidos por uma praga, uma delegação foi enviada ao oráculo de Apolo em Delos para perguntar como a peste poderia ser combatida. Este respondeu que para tanto o altar de Apolo, cuja forma era cúbica, deveria ser dobrado. Uma outra versão diz que o rei Minos insatisfeito com o tamanho do túmulo de seu filho Glauco ordenou que o túmulo fosse dobrado, porém sem que perdesse a forma original.
Os gregos obviamente estavam familiarizados com um problema semelhante, porém bem mais simples: duplicar o quadrado.
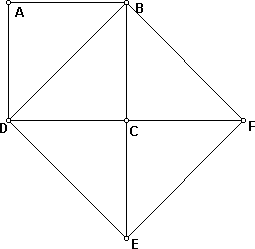
Dado um quadrado ABCD, traçar a sua diagonal BD e construir um quadrado de lado BD. É fácil perceber que BDEF tem o dobro da área de ABCD. Assim dado um quadrado de lado a é possível encontrar um outro quadrado de lado b cuja área seja o dobro da área do primeiro, portanto
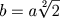
(onde b é a diagonal do quadrado original).
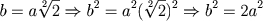
Talvez tenha sido esta simples construção que levou os gregos a pensarem em uma solução para o problema da duplicação do cubo.
O primeiro grande passo foi dado por Hipócrates de Chios, provavelmente não muito depois da aparição do problema. Ele propunha encontrar duas médias proporcionais entre segmentos de comprimento s e 2s, ou seja, achar x e y tal que:
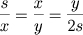
Da primeira igualdade deduzimos que
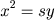
e da segunda igualdade que
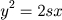
. Substituindo o valor de y na segunda igualdade temos que
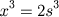
. Assim dado o cubo de lado s encontramos um outro de lado x tal que o volume do segundo é o dobro do volume do primeiro. Porém não há construção geométrica para esta dupla proporção.
Também devemos considerar a solução proposta por Arquitas de Tarento, à respeito da qual Heath [Heath, 1931] escreveu:
"A solução de Arquitas é a mais notável de todas, especialmente quando sua data é considerada (primeira metade do séc IV a.C.) porque não é nenhuma construção plana mas uma corajosa construção em três dimensões, determinando um certo ponto como a intersecção de três superfícies de revolução..."
Entretanto todas as soluções eram teóricas e nenhuma solução pratica foi encontrada.
Apenas no séc XIX , mais de 2000 anos depois da formulação do problema foi que se estabeleceu a impossibilidade da construção sob a limitação de usar apenas régua e compasso (instrumentos euclideanos).





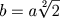 (onde b é a diagonal do quadrado original).
(onde b é a diagonal do quadrado original).
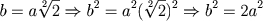
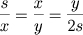
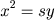 e da segunda igualdade que
e da segunda igualdade que 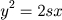 . Substituindo o valor de y na segunda igualdade temos que
. Substituindo o valor de y na segunda igualdade temos que 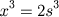 . Assim dado o cubo de lado s encontramos um outro de lado x tal que o volume do segundo é o dobro do volume do primeiro. Porém não há construção geométrica para esta dupla proporção.
Também devemos considerar a solução proposta por Arquitas de Tarento, à respeito da qual Heath [Heath, 1931] escreveu:
"A solução de Arquitas é a mais notável de todas, especialmente quando sua data é considerada (primeira metade do séc IV a.C.) porque não é nenhuma construção plana mas uma corajosa construção em três dimensões, determinando um certo ponto como a intersecção de três superfícies de revolução..."
Entretanto todas as soluções eram teóricas e nenhuma solução pratica foi encontrada.
Apenas no séc XIX , mais de 2000 anos depois da formulação do problema foi que se estabeleceu a impossibilidade da construção sob a limitação de usar apenas régua e compasso (instrumentos euclideanos).
. Assim dado o cubo de lado s encontramos um outro de lado x tal que o volume do segundo é o dobro do volume do primeiro. Porém não há construção geométrica para esta dupla proporção.
Também devemos considerar a solução proposta por Arquitas de Tarento, à respeito da qual Heath [Heath, 1931] escreveu:
"A solução de Arquitas é a mais notável de todas, especialmente quando sua data é considerada (primeira metade do séc IV a.C.) porque não é nenhuma construção plana mas uma corajosa construção em três dimensões, determinando um certo ponto como a intersecção de três superfícies de revolução..."
Entretanto todas as soluções eram teóricas e nenhuma solução pratica foi encontrada.
Apenas no séc XIX , mais de 2000 anos depois da formulação do problema foi que se estabeleceu a impossibilidade da construção sob a limitação de usar apenas régua e compasso (instrumentos euclideanos).