O processo para o cálculo do comprimento da circunferência, que é
apresentado na obra
Sobre as medidas do círculo, é considerado
a primeira tentativa verdadeiramente científica de calcular o valor
aproximado de
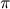
. Primeiro
Arquimedes
considerou uma circunferência com um hexágono inscrito e outro
circunscrito à ela e calculou os comprimentos de seus respectivos
perímetros.
Como o comprimento da circunferência está entre estes dois valores,
obtém-se assim uma aproximação por deficiência e outra por excesso
para o valor de
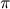
.
Nesta época já se conhecia uma fórmula que permitia calcular, a partir
do valor do perímetro de um polígono regular, o perímetro de outro com
o dobro do número de lados. Utilizando-se desta fórmula,
Arquimedes calcula perímetros de polígonos inscritos e
circunscritos de 12, 24, 48 e 96 lados, chegando à conclusão de que o
valor de
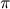
deve estar situado entre
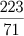
e
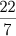
(em notação decimal com aproximação de duas casas
eqüivale a dizer que
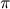
vale 3,14).
Este método é conhecido como o
método clássico para a
determinação de
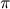
.




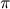 . Primeiro Arquimedes
considerou uma circunferência com um hexágono inscrito e outro
circunscrito à ela e calculou os comprimentos de seus respectivos
perímetros.
Como o comprimento da circunferência está entre estes dois valores,
obtém-se assim uma aproximação por deficiência e outra por excesso
para o valor de
. Primeiro Arquimedes
considerou uma circunferência com um hexágono inscrito e outro
circunscrito à ela e calculou os comprimentos de seus respectivos
perímetros.
Como o comprimento da circunferência está entre estes dois valores,
obtém-se assim uma aproximação por deficiência e outra por excesso
para o valor de 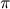 .
Nesta época já se conhecia uma fórmula que permitia calcular, a partir
do valor do perímetro de um polígono regular, o perímetro de outro com
o dobro do número de lados. Utilizando-se desta fórmula, Arquimedes calcula perímetros de polígonos inscritos e
circunscritos de 12, 24, 48 e 96 lados, chegando à conclusão de que o
valor de
.
Nesta época já se conhecia uma fórmula que permitia calcular, a partir
do valor do perímetro de um polígono regular, o perímetro de outro com
o dobro do número de lados. Utilizando-se desta fórmula, Arquimedes calcula perímetros de polígonos inscritos e
circunscritos de 12, 24, 48 e 96 lados, chegando à conclusão de que o
valor de 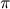 deve estar situado entre
deve estar situado entre 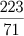 e
e
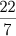 (em notação decimal com aproximação de duas casas
eqüivale a dizer que
(em notação decimal com aproximação de duas casas
eqüivale a dizer que 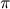 vale 3,14).
Este método é conhecido como o método clássico para a
determinação de
vale 3,14).
Este método é conhecido como o método clássico para a
determinação de 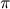 .
.