Ao longo da Baixa Idade Média, no Islam, os árabes tornaram-se patronos da cultura, traduzindo para
o árabe manuscritos hindus e gregos como
Os elementos de
Euclides, o
Almajesto de Ptolomeu, além de inúmeros trabalhos de astronomia, medicina e filosofia
grega, que posteriormente foram traduzidos para o latim e outras línguas por intelectuais
europeus. Em Bagdá foi criada a
Casa de Sabedoria comparável ao antigo Museu de Alexandria,
onde encontrava-se mestres, como o matemático e astrônomo Mohammed ibu-Musa Al-Khowârizmî (Maomé,
filho de Moisés de Khwarezm) que escreveu algumas obras de astronomia, tabelas sobre o astrolábio,
relógio do sol, aritmética e álgebra. Estas últimas, tiveram papeis importante na história da
matemática.
O livro
De numero hindorum (
Sobre a arte hindu de calcular) foi, provavelmente, baseado
numa tradução árabe de Brahmagupta, e trata de uma exposição completa dos numerais hindus. A
tradução para o latim desta obra contribuiu, na Europa, para a divulgação destes numerais que
posteriormente vieram à ser chamados de algorismos ou algoritmos, palavra que originalmente deriva
do nome de Al-Khowârizmî.
Seu livro mais importante foi
Al-jabr wa'l muqabalah, de onde se originou o termo álgebra.
Neste livro Al-Khowârizmî expressasse inteiramente com palavras, mesmos os números são escritos em
palavras em vez de símbolos. O texto contém uma exposição direta e elementar da resolução de
equações, especialmente de segundo grau.
Não se sabe os significados certos dos termos
al-jabr e
muqabalah, supõe-se que
al-jabr significa "restauração" ou "completação" e refere-se à transposição de termos
subtraídos para o outro lado da equação, a palavra
muqabalah significa "redução" ou
"equilíbrio" e refere-se à cancelamento de termos semelhantes em lados opostos da equação.
O
Al-jabr wa'l muqabalah chegou à nós em duas versões, a latina e a árabe. A tradução
latina inicia-se com uma exposição do princípio posicional para números e passa-se à resolução, em
seis capítulos, dos seis tipos de equações formadas com três espécies de quantidades: raízes,
quadrados e números (isto é,
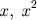
e números). Vamos detalhar um pouco o conteúdo destes
capítulos.
O capítulo I, abrange o caso dos quadrados iguais a raízes, que atualmente representamos como
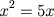
,
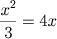
,
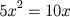
, etc., cujas respostas são,
respectivamente, x = 5, x = 12, x = 2. A raiz x = 0 não era reconhecida, assim como as raízes
negativas.
O capítulo II abrange o caso de quadrado iguais a números. O capítulo III resolve o caso de raízes
iguais a números, analisando os casos em que o coeficiente do termo variável é igual a um, menor
que um ou maior que um.
Os capítulos IV, V e VI abrange os três caso de equações quadráticas com três termos:
- quadrados e raízes iguais a números (
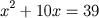 );
);
- quadrados e números iguais a raízes (
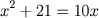 );
);
- raízes e números iguais a quadrados (
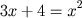 ).
).
As soluções apresentadas são regras práticas de "completar o quadrado" aplicadas a exemplos
específicos.
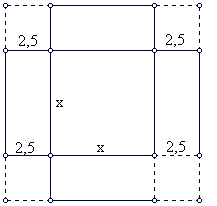
Al-Khowârizmî após expor e resolver as equações demonstra geometricamente seus resultados. Como
exemplo, a equação
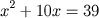
é representada por um quadrado de lado x, e sobre os quatro
lados construi-se retângulos de largura 2,5 unidades. Para completar o quadrado maior precisamos
construir quatro quadrados menores nos cantos da figura, cada um com área igual a 6,25 unidades.
Portanto para "completar o quadrado" somamos 4 vezes 6,25 unidades ou seja 25 unidades, obtemos
então um quadrado com área total 39 + 25 = 64. Concluímos que o lado do quadrado maior mede 8
unidades e se subtrairmos 2 vezes 2,5 unidades ou seja 5 unidades, achamos x = 3, o que comprova o
resultado obtido no capítulo IV.
Em
Al-jabr wa'l muqabalah encontramos também operações com expressões binomiais, as regras
que governam as operações com sinais (que atualmente chamamos de regras de sinais), problemas de
herança, além de outras demonstrações geométricas. A exposição de Al-Khowârizmî foi tão completa e
sistemática que ficou conhecido como o
pai da álgebra.
A Álgebra de Al-Khowârizmî é considerada a primeira obra sobre o assunto, e podemos dizer que ela
foi para a álgebra o que
Os elementos de
Euclides foi para a geometria -
a melhor exposição elementar disponível até os tempos modernos.




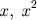 e números). Vamos detalhar um pouco o conteúdo destes
capítulos.
O capítulo I, abrange o caso dos quadrados iguais a raízes, que atualmente representamos como
e números). Vamos detalhar um pouco o conteúdo destes
capítulos.
O capítulo I, abrange o caso dos quadrados iguais a raízes, que atualmente representamos como
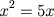 ,
, 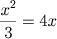 ,
, 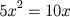 , etc., cujas respostas são,
respectivamente, x = 5, x = 12, x = 2. A raiz x = 0 não era reconhecida, assim como as raízes
negativas.
O capítulo II abrange o caso de quadrado iguais a números. O capítulo III resolve o caso de raízes
iguais a números, analisando os casos em que o coeficiente do termo variável é igual a um, menor
que um ou maior que um.
Os capítulos IV, V e VI abrange os três caso de equações quadráticas com três termos:
, etc., cujas respostas são,
respectivamente, x = 5, x = 12, x = 2. A raiz x = 0 não era reconhecida, assim como as raízes
negativas.
O capítulo II abrange o caso de quadrado iguais a números. O capítulo III resolve o caso de raízes
iguais a números, analisando os casos em que o coeficiente do termo variável é igual a um, menor
que um ou maior que um.
Os capítulos IV, V e VI abrange os três caso de equações quadráticas com três termos: 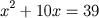 );
);
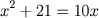 );
);
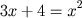 ).
).
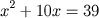 é representada por um quadrado de lado x, e sobre os quatro
lados construi-se retângulos de largura 2,5 unidades. Para completar o quadrado maior precisamos
construir quatro quadrados menores nos cantos da figura, cada um com área igual a 6,25 unidades.
Portanto para "completar o quadrado" somamos 4 vezes 6,25 unidades ou seja 25 unidades, obtemos
então um quadrado com área total 39 + 25 = 64. Concluímos que o lado do quadrado maior mede 8
unidades e se subtrairmos 2 vezes 2,5 unidades ou seja 5 unidades, achamos x = 3, o que comprova o
resultado obtido no capítulo IV.
é representada por um quadrado de lado x, e sobre os quatro
lados construi-se retângulos de largura 2,5 unidades. Para completar o quadrado maior precisamos
construir quatro quadrados menores nos cantos da figura, cada um com área igual a 6,25 unidades.
Portanto para "completar o quadrado" somamos 4 vezes 6,25 unidades ou seja 25 unidades, obtemos
então um quadrado com área total 39 + 25 = 64. Concluímos que o lado do quadrado maior mede 8
unidades e se subtrairmos 2 vezes 2,5 unidades ou seja 5 unidades, achamos x = 3, o que comprova o
resultado obtido no capítulo IV.
